Celia Castillo Martinez

Contents

EJERCICIO 1

apartado a

%function f = factr(n)
%if n == 0
%    f = 1;
%else
%    f = n * factr(n-1);
%end
%end

%Llamamos a la funcion con el nombre factr creado en el script con el mismo
%nombre, y lo evaluamos para n=4, por ejemplo.
factr(4)

ans =

    24

apartado b

%function f = combina(n,j)
%n:tamaño de la colección
%j:vector de cero a n
%a=n-j;
%f=factr(n)/(factr(j)*factr(a));
%end

%Llamamos a la funcion con el nombre combina creado en el script con el mismo
%nombre, y lo evaluamos para n=5 y j=2, por ejemplo
combina(5,2)

ans =

    10

apartado c

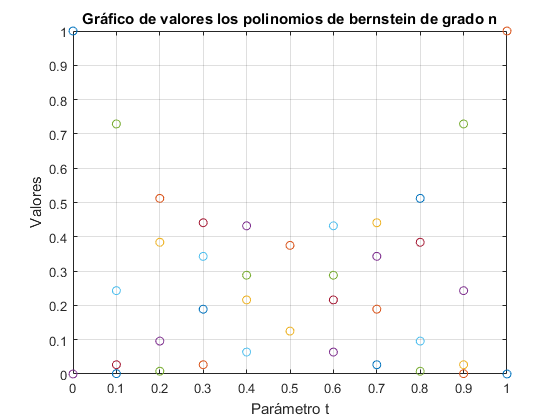
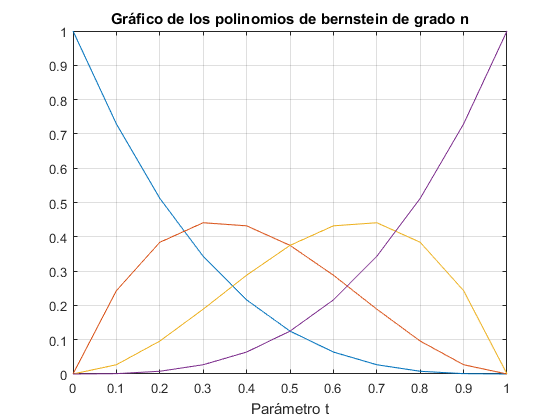
%function f=bernstein(n,t)
%Parámetro t, según se indica en el enunciado está en el intervalo [0,1]
%coef=[];
%for i=0:n
%    comb=combina(n,i);
%    a=n-i;
%    b=comb*t^i*(1-t)^a;
%    coef=[coef b];
%end
%f=coef'; %Muestra vector con los valores de los polinomios para un t determinado
%end

%Llamamos a la funcion con el nombre berstein creado en el script con el mismo
%nombre, y lo evaluamos para n=3 y t=0.5 por ejemplo.
bernstein(3,0.5)

% Función para el dibujo de los polinomios de grado 3 de Bernstein:
% function f=ber_vect(n,t)
% %Función que recurre a bernstein para dibujar los valores de los polinomios
% %en la misma gráfica
% %b=bernstein(n,t);%Vector con los valores del polinomio para un t
% m=length(t);
% b=[];
% for j=t
%    b1=bernstein(n,j);
%    b=[b b1];%Se guardan todos los valores de los polinomios
%    plot(j,b1,'o');hold on
% end
% grid on, title('Gráfico de los polinomios de bernstein de grado n');
% xlabel('Parámetro t');ylabel('Valores');
% end
%Ejemplo:
n=3;
t1=0:0.1:1;
ber_vectbueno(n,t1);

ans =

    0.1250
    0.3750
    0.3750
    0.1250

apartado d

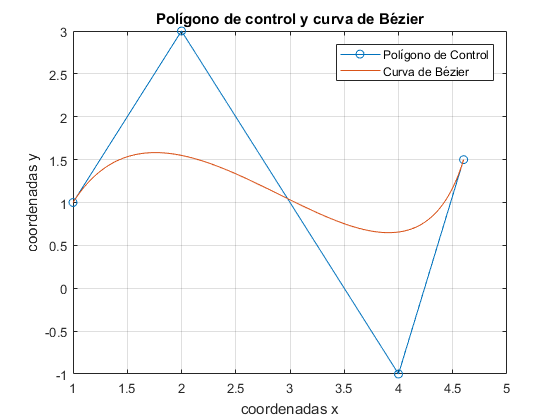
%Vectores:(de dos componentes: la curva es planar, por tanto)
vx=[1 2 4 4.6]';
vy=[1 3 -1 1.5]';
%Variación del parámetro t en 0.01
t=0:0.01:1;
%Representación del polígono de control:
figure(3)
plot(vx,vy,'-o');grid on, hold on;
title('Polígono de control y curva de Bézier'); xlabel('coordenadas x');ylabel('coordenadas y');
n=3;
%Por cada t se tiene un punto de coordenadas x,y
X1=[];Y1=[];
for j=t
    b=bernstein(n,j);
    x1=vx.*b;
    y1=vy.*b;
    %Vectores que guardan los valores de la curva de Bézier para cada i:
    X1=[X1 x1];
    Y1=[Y1 y1];
end
%Para guardar en un vector todos los valores de los sumatorios para cada t:
xx=[];yy=[];
for j=1:length(X1)
    xx=[xx;sum(X1(:,j))];
    yy=[yy;sum(Y1(:,j))];
end
plot(xx,yy);hold off
legend('Polígono de Control','Curva de Bézier');

EJERCICIO 2

apartado a

% Leer los datos de viento del fichero y hacer un histograma
% considerando intervalos de clase entre [0,25].
% Leer del rango B2:B52129
datos=xlsread('datosviento.xlsx','B2:B52129');
nbins=0:25;

%No se si esto funciona, es un intento de sacar los valores de frecuencia
%del histograma, aunque ha dejado de dibujarlo, seguir comprobando
figure(4)
hist(datos,nbins)
title('Histograma de frecuencias')
grid on

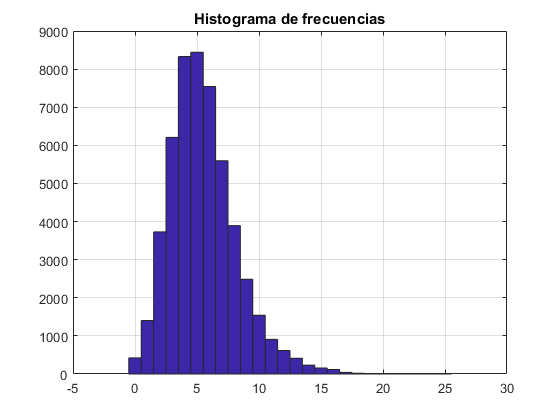
apartado b

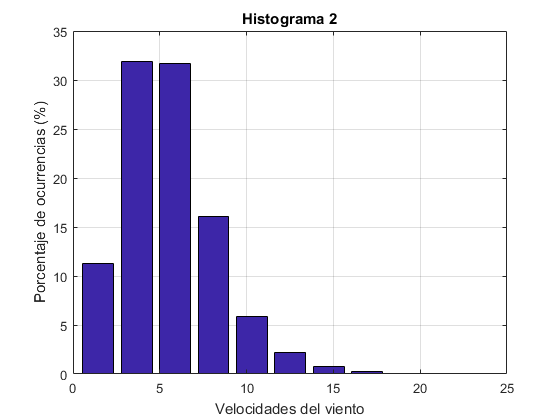
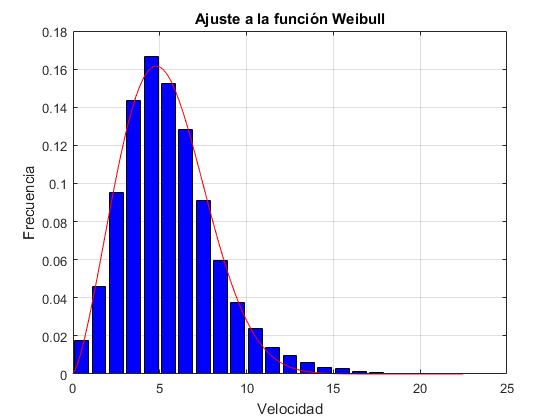
%Lectura de datos, gráfico del histograma de frecuencias y
%ajustes
%Lectura de datos:
lect1=xlsread('datosviento.xlsx');
velocidad=lect1(:,1);

%Interpolación si necesario
if any(isnan(velocidad)) %si hay algún NaN
    x=1:length(velocidad);
    i=find(~isnan(velocidad));
    velocidad=interp1(x(i),velocidad(i),x);
end

%Histograma de frecuencias
x=0.5:1:max(velocidad);
horas=hist(velocidad,x);
%Convierte a frecuencias
frec=horas/sum(horas);
[n xout]=hist(velocidad);
bar(xout,n*100/length(lect1));grid on,
title('Histograma 2')
xlabel('Velocidades del viento')
ylabel('Porcentaje de ocurrencias (%)');

%Ajuste a la función de Weibull
modelfunc=@(a,x) (a(1)/a(2))*((x/a(2)).^(a(1)-1)).*exp(-(x/a(2)).^a(1));
beta0=[mean(velocidad) std(velocidad)];%Valores iniciales de los parámetros
beta=nlinfit(x,frec,modelfunc,beta0);
%Parametros de Weibull
k=beta(1);, c=beta(2);
fprintf('Parámetros Weibull: k=%1.4f, c=%1.4f\n',k,c)

%Gráfica del ajuste

%diagrama de frecuencias
figure(5)
bar(x,frec,'b');grid on;hold on
%representa la curva de ajuste
x=linspace(0,max(velocidad),100);
y=modelfunc(beta,x);
plot(x,y,'r')
title('Ajuste a la función Weibull')
xlabel('Velocidad')
ylabel('Frecuencia')
hold off

Parámetros Weibull: k=2.3849, c=6.0208

apartado c

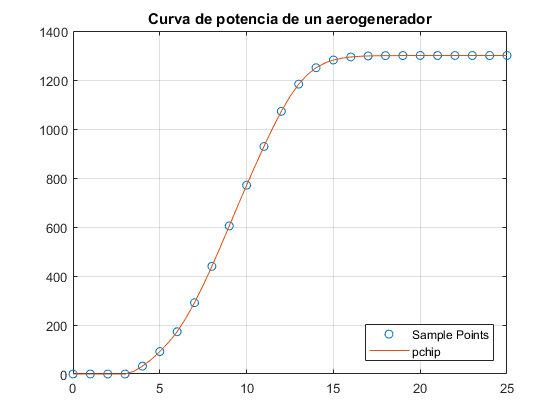
% Leer los datos x e y del archivo de excel
x=xlsread('datospotencia','A2:A27');
y=xlsread('datospotencia','B2:B27');

%Puntos de la interpolación entre 0 y 25 en intervalos de 0.5
xq1 = 0:0.5:25;
p = pchip(x,y,xq1);

figure(6)
plot(x,y,'o',xq1,p,'-')
grid on
title('Curva de potencia de un aerogenerador')
legend('Sample Points','pchip','Location','SouthEast')

apartado d

%Script que agrupa los dos apartados anteriores e introduce la integración por quad
%directamente de los datos de las velocidades del viento
potencia=0.5*1.225*sum(velocidad.^3)/length(velocidad);
fprintf('Potencia, directamente de las medidas: %3.1f\n',potencia);
media=mean(velocidad);
%función de distribución de Weibull
potencia=0.5*1.225*media^3*gamma(1+3/k)/(gamma(1+1/k)^3);
fprintf('Potencia, función Weibull: %3.1f\n',potencia);


%Potencia media con quad

%datos de la curva de potencia
%Sacados de los datos de potencia del excel

Pr=1300; x0=4.0;xr=20;x1=25;

%Valores de los parametros de Weibull
k=2.3849;
c=6.0208;

potencia=xlsread('datospotencia.xlsx','B2:B27');
x=0:1:25;
pot=potencia(x>=x0 & x<=xr);

x=x0:1:xr;

%Ajuste
p=polyfit(x,pot',3); %ajuste a un polinomio de tercer grado
yp=polyval(p,x);

%cálculo de la potencia media
f=@(x) (k/c)*((x/c).^(k-1)).*exp(-(x/c).^k); %función de Weibull
h=@(x) f(x).*polyval(p,x);
power=quad(h,x0,xr)+Pr*quad(f,xr,x1);
fprintf('La potencia media es: %3.1f\n',power)

Potencia, directamente de las medidas: 187.8
Potencia, función Weibull: 170.0
La potencia media es: 199.1

EJERCICIO 3

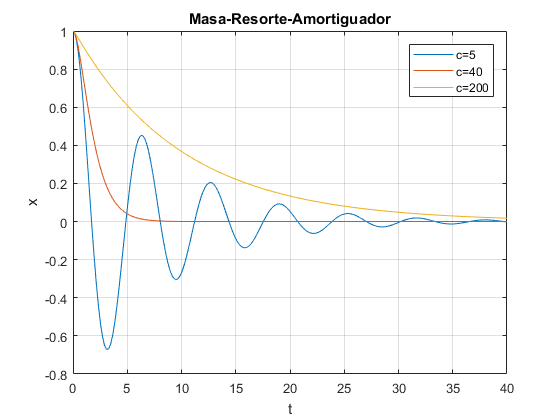
Resolver la ecuación diferencial mediante el solver ODE RK (ode45) para un periodo de 40 seg. Graficar en una misma gráfica el desplazamiento en función del tiempo para cada uno de los valores del coeficiente de amortiguamiento: 5, 40, 200 Sujeta a las condiciones iniciales: m=20 Kg k=20N/m V0=0 m/s X0=1m

figure(7)

m=20;
k=20;
x0=[1,0]; %1 es posicion inicial y 0 es velocidad inicial
tf=40; %Quiero graficar de 0 a 40 segundos
c1=5;
c2=40;
c3=200;

%Indico cual es la funcion
%x(1) es x y x(2) es v
%Luego el punto y coma sirve como separador de ambos miembros (funciones a integrar)

f1=@(t,x) [x(2);(-k*x(1)-c1*x(2))/m];
f2=@(t,x) [x(2);(-k*x(1)-c2*x(2))/m];
f3=@(t,x) [x(2);(-k*x(1)-c3*x(2))/m];

[t1,x1]=ode45(f1,[0,tf],x0);
[t2,x2]=ode45(f2,[0,tf],x0);
[t3,x3]=ode45(f3,[0,tf],x0);
%Dibujo la grafica de x en funcion de t para c=5

plot(t1,x1(:,1))
grid on
xlabel('t');
ylabel('x');
title('Masa-Resorte-Amortiguador');

%Para dibujar todas las graficas juntas
hold on;

%Grafica para c=40
plot(t2,x2(:,1))
%Grafica para c=200
plot(t3,x3(:,1))

legend('c=5','c=40', 'c=200')

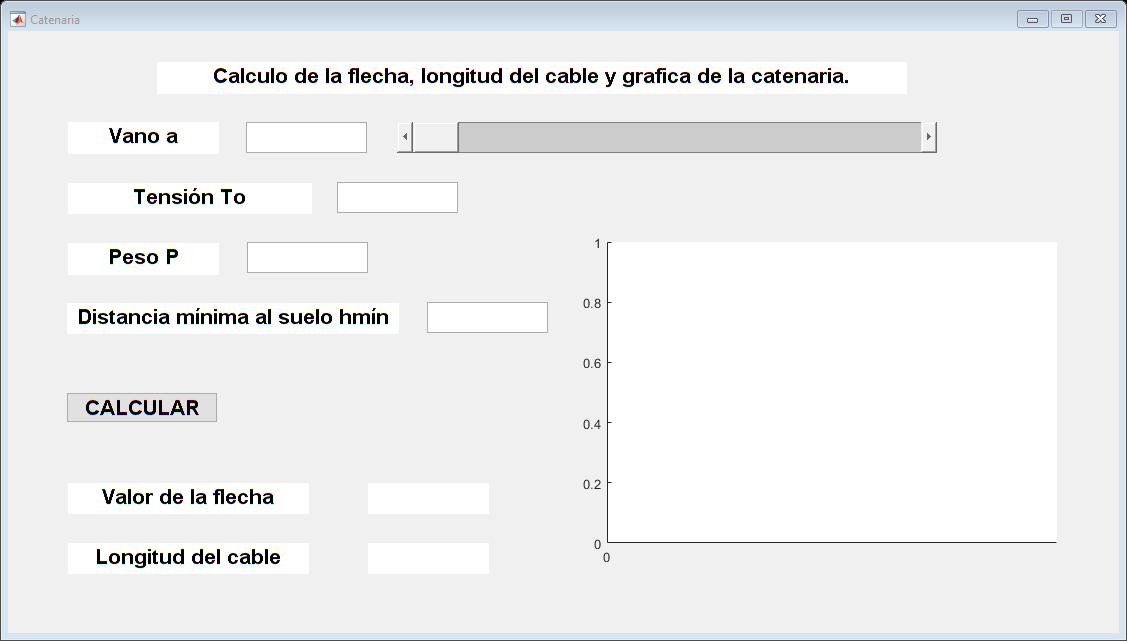
EJERCICIO 4 GUI

%El script en el que se pide realizar una GUI para calcular la fecha y
%la longitud de una catenaria y graficar la misma, esta incluido en el zip
%con el resto de ejercicios, asi como la imagen de la grafica.
%No he podido introducirlo en la tarea, me daba un error y no funconaba
%supongo que es normal pues tiene que interactuar con el usuario y en el
%publish tampoco se hubiera podido hacer

Catenaria

Published with MATLAB® R2017a